K-D Tree 学习笔记

头图什么的放一边了。
(以后回来整理())

起因是写邻域查询得知查询时间复杂度是 $O (n)$ ，感觉没啥动力写了，于是就整理一下了 QAQ。

K-D Tree

K-D 树 是一种可以维护 $k$ 维空间一些信息的数据结构。以 MnZn 的视角看，可以做多维偏序相关问题。但具体哪些可以、哪些不可以（还是靠试一下 awa）

K-D 树 是维护了 $k$ 维空间若干个点的一棵平衡树。

等等， $k$ 维空间两点怎么比较大小啊喂，它甚至不是二叉搜索树吧！

欸，你 $k$ 维空间一个点不是用 $k$ 个数值表示的吗，比如 $(1, 2)$ 、 $(5, 1, 4)$ ，那么我的树上深度第 $s$ 层就按照 $(s \mod k) + 1$ 个数值来分割左右子树。

听起来很有意思，又过于直觉了。

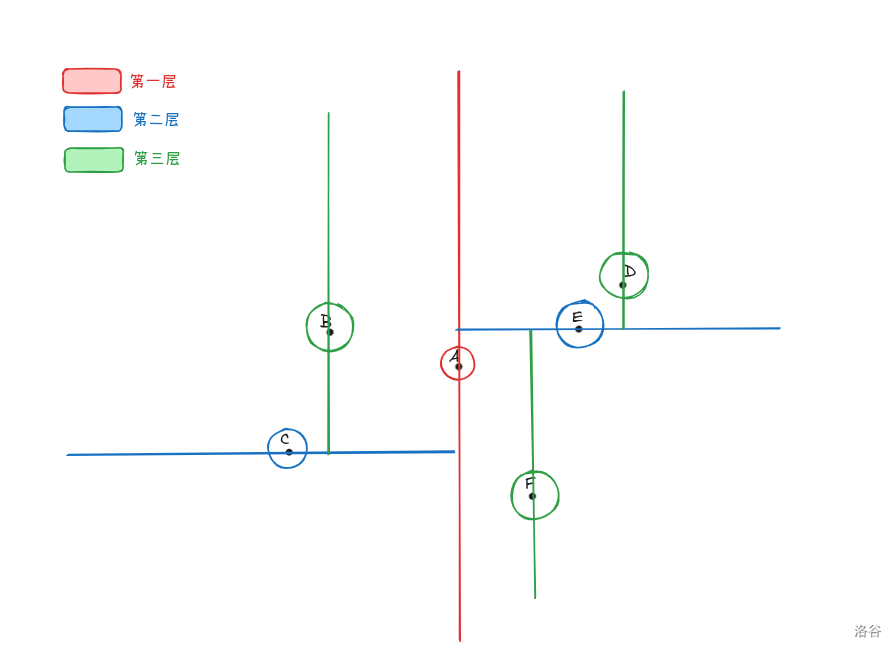
不过先图解一下二维的分割方法吧。

嗯，比较直观了 111。

由于 OI 上一般都是二维问题使用，所以接下来的描述默认为 2-D Tree。

性质

过于直觉的点在于，这样做树高是平衡的吗？有啥良好的性质吗？

首先，你每次其实是取该维度坐标的中位数作为这一层的点，分割出左右子树，那么这就是二分了，所以树高是 $\log n + O (1)$ 的。

其次，这棵树的一个节点的子树对应这一个矩形，描述矩形的端点可以由 Push_up 得到。

性质决定用途：对于矩形查询操作就比较类似线段树的区间查询操作的写法了。

但是，插入操作怎么办，插入后怎么才能平衡呢。

比较常见的是替罪羊树和朝鲜树的重构写法（在 $\geq 4$ 年前的题解常见）。

但都是假的。

根号重构和二进制分组才是对的。

那么就可以写出第一份自己的 KDT：

Luogu P4148 简单题

cpp

#include<bits/stdc++.h>
#define reg register
#define rep(i,a,b) for(reg int (i)=(a);(i)<=(b);++(i))
#define drep(i,a,b) for(reg int (i)=(a);(i)>=(b);--(i))
#define il inline
#define pb push_back
#define ins insert
#define ll long long
using namespace std;
const int N=5e5+10,MAXM=18;
struct Tree{
  int x[2];
  int v,sum;
  int l,r;
  int L[2],R[2];
}t[N],l,h;
int b[N],rt[MAXM],cnt;
inline void pushup(reg int p){
    t[p].sum=t[t[p].l].sum+t[t[p].r].sum+t[p].v;
    for(auto k:{0,1}){
        t[p].L[k]=t[p].R[k]=t[p].x[k];
        if(t[p].l){
            t[p].L[k]=min(t[p].L[k],t[t[p].l].L[k]);
            t[p].R[k]=max(t[p].R[k],t[t[p].l].R[k]);
        }
        if(t[p].r){
            t[p].L[k]=min(t[p].L[k],t[t[p].r].L[k]);
            t[p].R[k]=max(t[p].R[k],t[t[p].r].R[k]);
        }
    }
}
inline void rm(reg int &p){
    if(!p)return;
    b[++cnt]=p;
    rm(t[p].l);
    rm(t[p].r);
    p=0;
}
inline int bd(reg int l,reg int r,reg int dep=0){
    int mid=l+r>>1;
    nth_element(b+l,b+mid,b+r+1,[dep](reg int x,reg int y){
        return t[x].x[dep]<t[y].x[dep];
    });
    reg int p=b[mid];
    if(l<mid)t[p].l=bd(l,mid-1,dep^1);
    if(mid<r)t[p].r=bd(mid+1,r,dep^1);
    pushup(p);
    return p;
}
inline int qry(reg int p){
    if(!p)return 0;
    reg bool flag;
    flag=1;
    for(auto k:{0,1})flag&=(l.x[k]<=t[p].L[k]&&t[p].R[k]<=h.x[k]);
    if(flag)return t[p].sum;
    for(auto k:{0,1})if(t[p].R[k]<l.x[k]||h.x[k]<t[p].L[k])return 0;
    flag=1;
    for(auto k:{0,1})flag&=(l.x[k]<=t[p].x[k]&&t[p].x[k]<=h.x[k]);
    return t[p].v*flag+qry(t[p].l)+qry(t[p].r);
}
signed main(){
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    int n,op,lastans=0;cin>>n;n=0;
    while(1){
        cin>>op;
        if(op==1){
            int x,y,A;cin>>x>>y>>A;
            x^=lastans,y^=lastans,A^=lastans;
            t[++n]={{x,y},A};b[cnt=1]=n;int k=0;
            while(1){
                if(!rt[k]){
                    rt[k]=bd(1,cnt);
                    break;
                }else rm(rt[k]);
                ++k;
            }
        }else if(op==2){
            cin>>l.x[0]>>l.x[1]>>h.x[0]>>h.x[1];
            l.x[0]^=lastans,l.x[1]^=lastans;
            h.x[0]^=lastans,h.x[1]^=lastans;
            lastans=0;rep(i,0,MAXM-1)lastans+=qry(rt[i]);
            cout<<lastans<<'\n';
        }else break;
    }
    return 0;
}

邻域查询

呜啊啊，那么 K-D Tree 比较正经的用途（矩形）就比较局限了，因为查询是根号的。

（吐血，原来是个根号算法（喜

（（当然还有不正经的用途

骗分！

K-D Tree 在邻域查询单次查询通过剪枝实际表现可以和 $\log$ 算法相提并论，但实际最坏复杂度是 $O (n)$ 的，（没见到可以被卡到这个级别的题目，基本都是因为 KDT 跑得慢一点被卡了）。

我们通过计算到子树矩形的最短距离来作为估价函数 $f$ ，加上几个剪枝，就能在邻域查询获得不错的耗时。

Luogu P1429 平面最近点对

cpp

#include<bits/stdc++.h>
#define reg register
#define rep(i,a,b) for(reg int (i)=(a);(i)<=(b);++(i))
#define drep(i,a,b) for(reg int (i)=(a);(i)>=(b);--(i))
#define il inline
#define pb push_back
#define ins insert
#define ll long long
using namespace std;
const int N=2e5+10,MAXM=18;
struct Tree{
  double x[2];
  int l,r;
  double L[2],R[2];
}t[N];
inline void pushup(reg int p){
    for(auto k:{0,1}){
        t[p].L[k]=t[p].R[k]=t[p].x[k];
        if(t[p].l){
            t[p].L[k]=min(t[p].L[k],t[t[p].l].L[k]);
            t[p].R[k]=max(t[p].R[k],t[t[p].l].R[k]);
        }
        if(t[p].r){
            t[p].L[k]=min(t[p].L[k],t[t[p].r].L[k]);
            t[p].R[k]=max(t[p].R[k],t[t[p].r].R[k]);
        }
    }
}
inline int bd(reg int l,reg int r){
    if(l>r)return 0;
    if(l==r){pushup(l);return l;}
    reg int mid=l+r>>1;reg double bl=0,br=0,sl=0,sr=0;
    rep(i,l,r)bl+=t[i].x[0],br+=t[i].x[1];
    bl/=1.0*(r-l+1),br/=1.0*(r-l+1);
    rep(i,l,r)sl+=1.0*(t[i].x[0]-bl)*(t[i].x[0]-bl),sr+=1.0*(t[i].x[1]-br)*(t[i].x[1]-br);
    if(sl>sr)nth_element(t+l,t+mid,t+r+1,[](reg Tree x,reg Tree y){return x.x[0]<y.x[0];});
    else nth_element(t+l,t+mid,t+r+1,[](reg Tree x,reg Tree y){return x.x[1]<y.x[1];});
    t[mid].l=bd(l,mid-1);t[mid].r=bd(mid+1,r);
    pushup(mid);
    return mid;
}
double ans=1e18;
double f(reg int a,reg int b){
    reg double res=0;
    if(t[a].x[0]<t[b].L[0])res+=1.0*(t[a].x[0]-t[b].L[0])*(t[a].x[0]-t[b].L[0]);
    if(t[a].x[0]>t[b].R[0])res+=1.0*(t[a].x[0]-t[b].R[0])*(t[a].x[0]-t[b].R[0]);
    if(t[a].x[1]<t[b].L[1])res+=1.0*(t[a].x[1]-t[b].L[1])*(t[a].x[1]-t[b].L[1]);
    if(t[a].x[1]>t[b].R[1])res+=1.0*(t[a].x[1]-t[b].R[1])*(t[a].x[1]-t[b].R[1]);
    return res;
}
double dis(reg int a,reg int b) {
    return 1.0*(t[a].x[0]-t[b].x[0])*(t[a].x[0]-t[b].x[0])+1.0*(t[a].x[1]-t[b].x[1])*(t[a].x[1]-t[b].x[1]);
}
void qry(int l,int r,int x){
    if(l>r)return;
    int mid=l+r>>1;
    if(mid!=x)ans=min(ans,dis(mid,x));
    if(l==r)return;
    double dl=f(x,t[mid].l),dr=f(x,t[mid].r);
    if(dl<ans&&dr<ans){
        if(dl<dr){
            qry(l,mid-1,x);
            if(dr<ans)qry(mid+1,r,x);
        }else{
            qry(mid+1,r,x);
            if(dl<ans)qry(l,mid-1,x);
        }
    }else{
        if(dl<ans)qry(l,mid-1,x);
        if(dr<ans)qry(mid+1,r,x);
    }
}
signed main(){
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    int n;cin>>n;rep(i,1,n)cin>>t[i].x[0]>>t[i].x[1];
    bd(1,n);rep(i,1,n)qry(1,n,i);printf("%.4lf\n",sqrt(ans));
    return 0;
}